Gianni78bari
Nuovo Utente
- Registrato
- 16/2/17
- Messaggi
- 151
- Punti reazioni
- 29
Tutti i post in ordine, senza dover cercare in archivio, si trovano anche qui: Giovanni Berardi – Medium
Siamo dunque giunti all'equazione di B&S che per costruzione elimina sia l'elemento di incertezza legato al prezzo dell'opzione (cioè il fattore (dW) casuale che influenzerebbe altrimenti l'opzione) che il rendimento u del sottostante che è presente nel modello di prezzo del sottostante stesso, ma quando viene portato da quest'ultimo nell'equazione che abbiamo costruito viene “semplificato via” assieme al fattore dW. Non abbiamo quindi bisogno di fare speculazioni relative ai rendimenti del sottostante.
Otteniamo alla fine una equazione differenziale parziale (PDE) cioè un'equazione matematica che coinvolge
a)più variabili indipendenti,
b)una funzione sconosciuta che dipende da tali variabili
c)derivate parziali della funzione sconosciuta rispetto alle variabili indipendenti.
Risolvendo per il prezzo dell'opzione otteniamo le formule della call e della put a seconda che poniamo le condizioni per ottenere il prezzo di una o dell'altra.
Ora possiamo analizzare l'equazione riscrivendola in modo più significativo
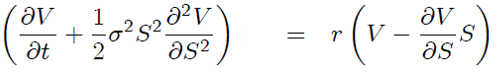
sappiamo inoltre che:
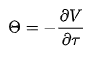
cioè che il primo addendo del membro a sinistra dell'equazione di black&scholes non è altro che la variazione del prezzo dell'opzione V rispetto alla variazione del tempo ovvero la greca theta
e sappiamo che:
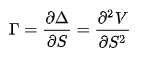
cioè che il secondo addendo del membro a sinistra dell'equazione è dato dalla variazione di delta rispetto a quella del sottostante, ovvero il gamma, moltiplicato per volatilità e sottostante al quadrato, il tutto diviso 2.
Ergo sostituendo abbiamo:
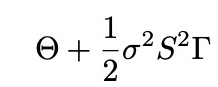
Poichè l'espressione sopra la eguagliamo al rendimento del portafoglio risk free a destra dell'equazione sopra che rimane statico, allora va da sé che theta e gamma devono avere andamento opposto.
In particolare possiamo definire la relazione tra theta e gamma dall'espressione appena ricavata:
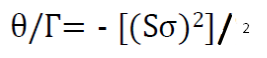
Sappiamo che il gamma è amico del compratore di opzioni perchè accelera i guadagni se il prezzo ci sorride e frena le perdite se il prezzo ci viene contro.
Allora la relazione sopra ci dice che per comprare gamma dobbiamo pagare in termini di theta un prezzo che aumenta col quadrato della volatilità e del sottostante. Quindi maggiore è la volatilità o il prezzo del sottostante e più grande sarà l'esborso per assicurarci il vantaggio di gamma (a parità di scadenza).
E viceversa: maggiore la volatilità più a caro prezzo potremo vendere il rischio che ci sobbarchiamo da “venditori” di gamma.
Notare che nell'equazione compaiono theta e gamma oltre che delta, ma non vega proprio perchè nel modello la volatilità è costante e non è contemplato cambi nell'intervallo considerato.
L'equazione di B&S rende anche chiaro visivamente come si arriva all'approssimazione usata dai vecchi option trader per calcolare la variazione di prezzo di una opzione:
PREZZO AL TEMPO T0 +
DELTA* (variazione sottostante S) +
GAMMA * 1/2(variazione S)^2+
VEGA*variazione IV+
THETA*variazione tempo=
________________________
PREZZO AL TEMPO T1
Nel prossimo post verrà analizzata la formula per il calcolo del valore di una call.
Siamo dunque giunti all'equazione di B&S che per costruzione elimina sia l'elemento di incertezza legato al prezzo dell'opzione (cioè il fattore (dW) casuale che influenzerebbe altrimenti l'opzione) che il rendimento u del sottostante che è presente nel modello di prezzo del sottostante stesso, ma quando viene portato da quest'ultimo nell'equazione che abbiamo costruito viene “semplificato via” assieme al fattore dW. Non abbiamo quindi bisogno di fare speculazioni relative ai rendimenti del sottostante.
Otteniamo alla fine una equazione differenziale parziale (PDE) cioè un'equazione matematica che coinvolge
a)più variabili indipendenti,
b)una funzione sconosciuta che dipende da tali variabili
c)derivate parziali della funzione sconosciuta rispetto alle variabili indipendenti.
Risolvendo per il prezzo dell'opzione otteniamo le formule della call e della put a seconda che poniamo le condizioni per ottenere il prezzo di una o dell'altra.
Ora possiamo analizzare l'equazione riscrivendola in modo più significativo
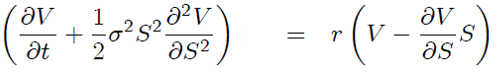
sappiamo inoltre che:
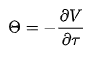
cioè che il primo addendo del membro a sinistra dell'equazione di black&scholes non è altro che la variazione del prezzo dell'opzione V rispetto alla variazione del tempo ovvero la greca theta
e sappiamo che:
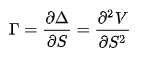
cioè che il secondo addendo del membro a sinistra dell'equazione è dato dalla variazione di delta rispetto a quella del sottostante, ovvero il gamma, moltiplicato per volatilità e sottostante al quadrato, il tutto diviso 2.
Ergo sostituendo abbiamo:
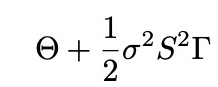
Poichè l'espressione sopra la eguagliamo al rendimento del portafoglio risk free a destra dell'equazione sopra che rimane statico, allora va da sé che theta e gamma devono avere andamento opposto.
In particolare possiamo definire la relazione tra theta e gamma dall'espressione appena ricavata:
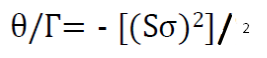
Sappiamo che il gamma è amico del compratore di opzioni perchè accelera i guadagni se il prezzo ci sorride e frena le perdite se il prezzo ci viene contro.
Allora la relazione sopra ci dice che per comprare gamma dobbiamo pagare in termini di theta un prezzo che aumenta col quadrato della volatilità e del sottostante. Quindi maggiore è la volatilità o il prezzo del sottostante e più grande sarà l'esborso per assicurarci il vantaggio di gamma (a parità di scadenza).
E viceversa: maggiore la volatilità più a caro prezzo potremo vendere il rischio che ci sobbarchiamo da “venditori” di gamma.
Notare che nell'equazione compaiono theta e gamma oltre che delta, ma non vega proprio perchè nel modello la volatilità è costante e non è contemplato cambi nell'intervallo considerato.
L'equazione di B&S rende anche chiaro visivamente come si arriva all'approssimazione usata dai vecchi option trader per calcolare la variazione di prezzo di una opzione:
PREZZO AL TEMPO T0 +
DELTA* (variazione sottostante S) +
GAMMA * 1/2(variazione S)^2+
VEGA*variazione IV+
THETA*variazione tempo=
________________________
PREZZO AL TEMPO T1
Nel prossimo post verrà analizzata la formula per il calcolo del valore di una call.